数理史上的绝妙证明：六角密堆积证明及其它

牛弎壮 2019-03-12 09:57:46 返朴未解之谜

六角密堆积是平面上最有效堆积方式的证明乃是人类历史上最天才的数学证明之一。

　　数学家图

　　阿克塞尔·图（Axel Thue， 1863-1922）是一位挪威数学家（图1），毕业于奥斯陆大学数学系，曾受数学名家索菲斯·李的指点，以丢番图方程、数论和组合方面的研究而闻名（比如证明了方程 y3 - 2x2 = 1 不可能有无穷多组整数解），被誉为思想与成就皆超前于时代的人。笔者以为，其1910年关于六角密堆积是平面上最有效堆积方式的证明乃是人类历史上最天才的数学证明之一，也是促成笔者撰写这本小册子的原因。这个证明不仅简洁、天才、惊艳，最重要的是该证明的哲学、技巧以及相关联的思考具有深刻的启发性意义。

图1。挪威数学家图

　　圆的密堆积

　　在桌面上摆放一把相同的圆形硬币，这会把我们引入平面上圆如何铺排（tessellation）的有趣问题。容易看到，一个硬币可以被六个硬币紧密环绕。所谓紧密的意思是，相邻三个硬币两两相接，形成一个正三角形；外围的六个硬币相互间是有接触的，没留下空隙（如图2）。把外围六个圆之间的接触点用直线段连起来，就得到一个围住中心圆的正六边形。如果我们只看这七个圆的圆心，它们的排列如图3中的七粒莲子所示（记住，大自然遵从数学和物理的规则！从前研究生物的人懂数学、物理、哲学和艺术，那时候统称博物学家），中间一个点，其余六个点在以其为中心的正六边形的六个顶点（vertex）上。图2中的圆在平面上的排列方式称为六角密堆积（hexagonal close packing）。容易计算，圆铺排的面积占比，用圆的面积除以相邻四个圆中心所张成的、边长为圆的直径而夹角为60°/120°的菱形的面积，为

。这样的排列方式，是最致密的。那么，如何证明呢？

图2。平面上圆的六角密堆积

图3。七粒莲子的长法，外围的六个处在围绕中心的正六边形的顶点上

　　六角密堆积的证明

　　阿克塞尔·图在1910年提供了一个非常简洁的但是意义深远的关于六角密堆积的证明。

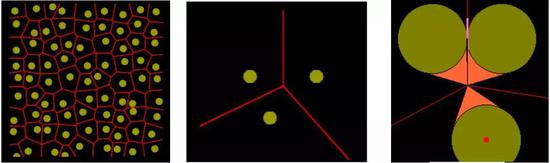
图4。（左）平面上随机分布的小圆，（中）近邻三小圆及其相互间的垂直平分线，（右）从垂直平分线的节点处向三小圆作切线，每个圆的两条切线在节点处张开一个相等的顶角

　　第一步

　　作为出发点，考虑图4左图中在平面内随机分布的诸多小圆，设想你往桌子上撒一把大小相同的豆豆，你就能得到这样的小圆在平面上的分布。

　　第二步

　　作任何一个小圆同近邻小圆之圆心连线的垂直平分线，会得到图4左图中的连线结构—每一个小圆都被一个凸多边形包围（一般为六边形。你如果没见过这样的图案，可以去观察干涸的河底泥巴断裂图案，或者去观察许多植物的叶脉。再强调一句，大自然遵从数学和物理的规则）。

　　第三步

　　观察第2步得到的连线结构，会注意到从每个连线节点发出的线段都是三条。考察每三个相邻小圆的连线问题，如果这三个小圆碰巧在一条直线上，则两两连线的垂直平分线是平行的。这样的三小圆构型不对理解二维的空间铺排问题有贡献，放过不管。看一般的情形（图4中图），近邻三小圆的三根两两之间连线的垂直平分线交于三小圆所张成之三角形内部的某个位置。

　　第四步

　　从垂直平分线的节点向三小圆作切线，共六条，容易证明每个圆的两条切线在节点处所张的顶角相等（图4右图），记为θ。但是，在平面内，3θ ≤ 360°，也即θ 的最大值为120°，这种情形对应的就是图1中圆的排列方式，故六角密排是最致密的排列方式。

　　QED。

　　细论图的证明

　　这个证明的天才、惊艳之处值得多啰嗦几句。

　　证明图2中的规则图案所对应的问题却从图4左图中的一般性随机图案出发，这个从方法论的角度来看就是了不起的举动。其所隐含的哲学意味也是有趣的——一个问题在更复杂的语境中反而是简单的。可以举一例说明。任意四个整数的平方乘以任意四个整数的平方，其积可以表示为四个整数的平方。如果只知道实数（含整数）和复数，这个问题的证明可能无从下手。但是，如果懂四元数的数学，则这个问题的证明就是个练习题而已。

　　从图4左图中的完全无规的分布出发，发现所有的节点都发出三条线，散乱无规的分布突然变得有规律了。这样，原来一个关于平面里的全局问题，变成了围绕一个点的局部问题。这告诉我们变换对问题的看法有多么重要。要不数学物理整天研究变换和变换不变性呢！

　　作相邻点连线的垂直平分线，想法有趣，结果意义深远。那么，人家是怎么想到要这么做的呢？笔者在给研究生讲授表面物理的时候，突然想到，这就是个发面的过程。设想图4左图中的每个小圆是一个发面团，随着烘烤的进行面团会向各方向扩张，则相邻两个面团最后达成的分界线就是两面团之间连线的垂直平分线（有兴趣的读者不妨去面包店看看托盘中烤好的面包边界所构成的图案，见图5）。图4左图中那些连线在小圆周围围成的多边形，称为伏龙诺伊单胞（Voronoi cell）。伏龙诺伊（Гео́ргий Феодо́сьевич Вороно́й，1868-1908）是俄罗斯数学家。图4中左图中的那些凸多边形，伏龙诺伊单胞，可以看作是对平面的划分方案。这个划分方案意义就大了，叶脉的分布（供水）、城市交通以及学校医院如何分布，不妨都参照一下这个划分方案。其实，图4中图中的三个小圆可连成一个三角形，别处也一样。这恰是对平面的三角化（triangulation）划分，这样做的合理性是建立在三角形的刚性上的。晶体可以看作是一堆原子占满了空间，作相邻原子连线的垂直平分面可以得到围绕每个原子的一个凸多面体，这个凸多面体是伏龙诺伊单胞的三维对应，被称为Wigner-Seitz 单胞。单胞结构和原来的点结构是对偶的（dual）。什么意思呢？你对空间中分布的物理量用函数 eikx 作傅里叶变换（晶体的X-射线衍射），所得结果在k-空间中也会有结构，那就是作空间中原子连线的垂直平分面所得到的结构。

图5。原先分立的面团经烘烤长大后，两面团边界就是面团中心连线的垂直平分线，这些垂直平分线围成的多边形就决定了面包的形状。

　　注意，平面六角密堆积和蜂窝结构非常容易混淆。平面六角密堆积中，堆积的对象是球，堆积成的结构被称为三角格子（triangular lattice），相邻的三个球之球心构成等边三角形。如果我们考察一个蜂窝（图6左图），把六角形的空巢当作主角，有蜂蛹的话可以拿蜂蛹作主角，会发现它们和图2的小球排列方式是一样的，属于三角格子。注意，这里的关键点是，这里每一个小蜂巢或者蜂蛹在空间上都是等价的。但是，如果我们考察蜂巢的壁，把蜂巢壁的节点当成主角的话，那就是常说的蜂窝结构。如果每个对应蜂窝结构的三条连线节点上放上一个炭[1]原子的话，那就是炭单层结构（图6右图）。这里的关键点是，相邻的两个炭原子是不等价的。对于蜂窝结构，也有蜂窝猜想，即蜂窝结构用料（蜂蜡）最省。翻译成几何语言，就是“将平面分割成多边形，在多边形面积一定的前提下，分成六角格子的分法（蜂窝形）所产生的多边形周长最短。”将多边形的面积设定为单位面积，则最短边长为

　　蜂窝猜想据说是古希腊人于约公元四世纪提出的，严格证明是美国数学家海尔斯（Thomas Hales，1958-）于1999年给出的。

图6。（左）峰巢或者其中的蜂蛹是主角的堆积方式是平面六角密堆积，属于三角格子；（右）六角形区域的三节点作为主角的堆积方式是蜂窝结构，属于六角格子。

　　平面内圆的密堆积问题在三维空间里对应的是球的密堆积。设想把球在平面内按照图2中的六角密堆积排成一层，记为A层。将同样的一层，B层，放到A层上，且每个B层的球落在A层中相邻三球围成的空隙中。现在考虑第三层， C层，的放法。选择1，C层的球落在B层的相邻三球围成的空隙中，但是位于A层球的正上方。换句话说，C层就是另一个A层。重复上述步骤，得到 ABABABAB… 形式的空间排列，这种排列方式是空间的六角密堆积（hexagonal close packing）。如 ZnS 一类的二元物质容易以两个异种原子为单元采取这种堆垛方式。选择2，C层的球落在B层的相邻三球围成的空隙，但也处于A层的相邻三球围成的空隙正上方。重复上述步骤，得到ABCABCABCABC…形式的空间排列，这种排列方式是空间的立方密堆积（cubic close packing）。一般单质金属如金、银、铜等的固体中，原子会采取立方密堆积的方式。固体物理上把这种结构称为面心立方。水果店里那些不是完美球形的水果也采取这种排列方式（走，观察去！）。这种结构的固体，虽然外观上易呈立方状，原子排列也有四次转动轴（转角90°），但是不要忘了它是由平面六角密堆积堆垛而来，那里的三次转动（转角120°）才是它的最高对称性。这两种堆垛方式有时就含糊地统称为空间的六角密堆积，它们的空间占比都是

[2]。

　　开普勒（Johannes Kepler， 1571-1630）猜测这样的堆垛方式是密度最大或者说空间占比最大的，这就是所谓的开普勒猜想（Kepler’s conjecture，1611年提出）。三维空间中球的密堆积问题来源于英国人关切球形炮弹的堆垛问题，面对按照六角密堆积堆出的外形不同的一堆炮弹，你能否脱口说出有多少发？生物体中有很多这种小球体（corpuscule）堆积而成的结构，可怜一些（故意装作）不懂数学的人儿，花费大量经费和时间用各种（不会用的）仪器研究这个问题，最后还是美国建筑学家富勒（Buckminster Fuller，1895-1983）告诉他们这种小问题不用那么努力认真研究，有现成的、特别简单的数学公式，口算一下就行了。

　　证明开普勒猜想，用阿克塞尔·图对付平面中圆密堆积的方法不凑效，因为包围单个球的凸多面体不是单一的——最小的凸多面体是正十二面体。不过，似乎也只有有限种选择，因此穷举法未必不是证明的思路。1831年，高斯证明了如果球必须按照规则的晶格排列（有平移对称性的排列），那开普勒猜想就是正确的。海尔斯的团队于1998 年宣布找到了证明，最后的证明于2017年发表在 Forum of Mathematics Pi 杂志上。

　　顺便说一句，有数学家认为阿克塞尔·图的证明不完备。完备性是数学证明里忒麻烦的东西，非笔者这样的非数学家可以讨论的。有关于平面圆密排定理的另一个证明，略述如下。将平面作捷洛内（Бори́с Никола́евич Делоне́，1890-1980） [3]三角划分，即将平面上单位圆的圆心连接使得平面被分割成一个一个的三角形（图7），可以证明这样的三角形，其内角必须在